Compass calibration on the water

Even if an electronic compass has been meticulously calibrated on land in a non-disturbed magnetic environment, it will need additional calibration adjustments once installed in a boat.

In a previous post, I described a procedure to recalibrate a compass with a GPS if you can find a patch of water where there is absolutely no current, a situation that practically does not exist in my maritime environment.

If your system can log the headings from a fast compass (5 Hz or more), here is an alternate method that can tolerate an existing current, but requires absolutely flat water (no waves) and no (or very negligible) wind. This is in fact the method that many commercial compass vendors choose to implement in their autocalibration routines, but presented here in a transparent manner.

These conditions must be met: a low and constant motoring speed (2 to 4 knots), and a tiller or wheel blocked in position so that a complete turn will take around 3 minutes.

Here is how I produced the results presented at the end of this post.

I made several turns while logging the headings (for both the Aimar H2183 and my own Hi-Resolution compass), as well as the boat speed. From the speed log, I find a section where the boat speed has been very stable, and I extract the heading data from a full turn.

We can make the reasonable hypothesis (with no waves and no wind) that our angular velocity has been constant during this golden turn, so that all recorded headings have to be separated by equal angles. If this is not the case, we can calculate the local deviation.

So several turns are recorded, but only the best one is used in the calibration. Here is simplified example using only a reduced set of measurements.

In Colum A, we have the measured headings on a complete turn, with 20 diffferent measurements. The expected angle difference between each measurement is 360/20 = 18 degrees. In Column B, we have calculated these expected headings if there was no deviation. In Column C, we calculate the deviation (A – B).

We can graph these deviations (C) vs. the measured heading (A). This is our deviation graph.

From these data points, we can calculate (using the NLREG software)  the 5 deviation coefficients (A, B, C, D, E) such as that:

Deviation = A + B sin(H) + C cos(H) + D sin(2*H) + E cos(2*H).

By correcting the measured heading by the calculated deviation, we obtain a pre-calibrated heading that still needs a last offset correction.  Our graph is based on the assumption that there is no deviation at our starting heading of 100 deg. But this is not necessarily the case; the zero-deviation point(s) may be at some other heading(s).

This last correction is easy to do, as we need only to compare any pre-calibrated heading value to a known heading. For example if, with the boat aligned along a dock at 78.0 deg, we obtain a pre-calculated heading of 76.5 deg, we will have to add a constant offset of 1.5 deg to all our pre-calibrated headings. (Don't trust your regular magnetic compass for this : it has its own uncorrected deviations).

Final corrected heading  =  Measured heading  - Deviation + Offset 


Here are the deviation curves obtained from my 2 compass, using data from the same turn.


Airmar H2183 Compass  (1721 meassurements, doubled 5 Hz samples ):

Hi-Resolution Compass (1737 measurements, 10 Hz samples):

 
So are we done?

Not really, because be still have to check if this calibration remains valid:
 - when the motor is not running
 - when the boat is heeling.

Getting an accurate magnetic heading is a never ending story.

Interfacing the Raymarine ST1000+ Autopilot

I understand that the Raymarine ST1000+ autopilot (and the similar ST2000+) can receive exterior heading data through the SeaTalk bus, specifically from a Raymarine ST40 fluxgate compass. So another project would be to use the heading output from my hi-resolution compass to drive the autopilot.

First I was interested to see what kind of data the autopilot puts on the SeaTalk bus as a talker. I used the following arrangement to monitor the SeaTalk bus.

The autopilot is connected to a serial port of a MAVRIC-IIB board through the SeaTalk interface circuit. The MAVRIC-IIB has an onboard MAX222 chip to provide level conversion between the serial port and the logic level pins of the ATMega128 microcontroller. The SeaTalk datagrams showing on the bus are resent in hex format to a computer running Hyperterminal, through a serial-to-USB converter.

The microcontroller code is an almost direct port of the “SeaTalk Monitor” code available on Thomas Knauf’s website. It can be found at the end of this post. In normal operation (standby or auto), the ST-1000+ sends continuously these 2 datagrams, each one at 1 Hz, with a half-second between them.

…
9C C1 07 00
84 C6 07 00 00 00 00 00 0F
9C C1 07 00
84 C6 07 00 00 00 00 00 0F
9C C1 07 00
84 C6 07 00 00 00 00 00 0F
9C C1 07 00
84 C6 07 00 00 00 00 00 0F
…

Here, the 9C datagram encodes the compass heading (in degrees) and the turning direction (left or right).

The 84 datagram also encodes the compass heading and turning direction, plus the autopilot course when in auto mode, and the currently active mode (standby, auto, vane or track mode).

We learn on Thomas Knauf’s site that the 89 datagram encodes the compass heading sent by the ST40 compass instrument, and can be read by the ST1000+ or ST2000+ autopilot. To test this behaviour, I modified the microcontroller code (not shown here) so that it sends an 89 datagram (89 02 04 00 20) after reading each of the 9C and 84 datagram, with a small delay to avoid collisions. The datagram sent (89 02 04 00 20) encodes a heading of 8 degrees.

The monitor then produced this kind of ouput:

…
9C 01 04 00
89 02 04 00 20
84 06 04 00 00 00 00 00 0F
89 02 04 00 20
9C 01 04 00
89 02 04 00 20
84 06 04 00 00 00 00 00 0F
89 02 04 00 20
…

From what I observed by playing with the autopilot in standby and auto mode, the 89 datagram is interpreted by the ST-1000+ as a request to perform a heading alignment to the value encoded in the datagram.

So if a custom heading is encoded in an 89 datagram sent on a regular basis, the autopilot will indeed adjusts its heading alignment if required to reproduce this value.


#include <avr/io.h>
#include <avr/interrupt.h>
#include <stdio.h>
unsigned char resh;
char buffer[256];
char hex[]="0123456789ABCDEF";
unsigned int collision_ctr;
unsigned char in_ptr, out_ptr, limit_ptr;
char receiver_buf, byte_ctr;

unsigned char kbhit(void)
{
 // return nonzero if char waiting
 unsigned char b;
 b = 0;
 if(UCSR1A & (1 << RXC1))
  b = 1;
 return b;
}

int uart_putchar0(char c)
{
 loop_until_bit_is_set(UCSR0A, UDRE0);
 UDR0 = c;
 return 0;
}

int main(void)
{
  in_ptr = 0;
  out_ptr = 0;
  limit_ptr = 0;

  /* enable serial port UART1 */  /* Set baud rate : 4800 @ 16 MHz */
  UBRR1L = (unsigned char)(207);
  /* Enable receiver with 9 data bits  */
  UCSR1B = _BV(RXEN1) | _BV(UCSZ12);

  /* enable serial port UART0 */  /* Set baud rate : 9600 @ 16 MHz */
  UBRR0L = (unsigned char)(103);
  /* Enable transmitter  */
  UCSR0B =_BV(TXEN0);
  for(;;)
  {
    if(kbhit())
    {
      // check 9th bit before reading UDR1
      resh = UCSR1B;
      resh = (resh >> 1) & 0x01;

      receiver_buf = UDR1;
 
      if(resh)     //  9th bit set
      {
        if(byte_ctr)   // More characters expected => Collision
        {
          in_ptr = limit_ptr;    // Discard last datagram, restart from beginning 
          collision_ctr++;     // Count collision events 
        }
        buffer[in_ptr++] = '\r';  // Put new command on new line 
        buffer[in_ptr++] = '\n';
        byte_ctr = 255;  // Undefined datagram length, wait for next character
      }
      else
      {
        if(byte_ctr == 254)       // Attribute byte ? 
        byte_ctr = (receiver_buf & 0xF) + 2; // Read expected datagram length
      }
      if(byte_ctr)
      {            // Process valid data bytes, should always be true 
        buffer[in_ptr++] = hex[receiver_buf >>  4]; // Convert Data to hex 
        buffer[in_ptr++] = hex[receiver_buf & 0xF];
        buffer[in_ptr++] = ' ';                     // Seperate by space 
        if(!--byte_ctr)
          limit_ptr = in_ptr;        // Complete datagram ready for output
      }
    }
    else
    {
      if(out_ptr != limit_ptr)          // Characters waiting for Output ?
      {
        // Copy single character from buffer to screen
        uart_putchar0(buffer[out_ptr++]);
      }
    }
  }
  return 1;
}

Building the 3 MHz ultrasonic transducer

A first 3 MHz transducer prototype is ready for testing. A vintage Airmar ST200 speed transducer housing has been modified to receive the piezoelectric element.

WARNING: this particular transducer design is not intended to be installed on a real boat for safety reasons. The threads between the compression ring and the housing may be stripped following an underwater impact, causing massive ingress of water. This design is intended to be used only for development purposes on special floating devices.

A future improvement will be to modify the form of the yellow urethane matching layer so as to get rid of the recess. This first prototype will be used mainly to test the electronics outside of a real boat, so that the safety epoxy plug will not be cast for the moment, in order to keep full access to the transducer.

I was fortunate to get the help of a competent machine shop owner to achieve this. Here are some pictures.

Designing an ultrasonic transducer

Here is the conceptual design of the 3-MHz ultrasonic transducer. Apart from the piezoelectric element, the 2 important design parameters are the nature of the backing and matching layers.

Air is a good absorber of high-frequency ultrasounds, and has been chosen as backing layer. The matching layer will be a sheet of urethane (40 A Durometer), available from this source.

The first step has been to characterize the piezoelectric element. Two wires have been soldered to the piezo’s silver platings.

The following arrangement has been used to measure the resonance and antiresonance frequencies of the piezo disc. The frequency generator is first adjusted to give a maximum voltage across the resistor: this is the resonant frequency, where the piezo impedance is at its minimum. The frequency is then increased until a minimum voltage is measured: this is the antiresonance frequency, where the impedance is at its maximum.

The results of these measurements are as follows:

            Resonance frequency:           2,932,000 Hz
            Antiresonance frequency:     3,345,000 Hz

The resonance frequency is where the piezo element converts with the highest efficiency the electrical energy into mechanical energy. This will be the design frequency of the transducer. Note that these frequencies are for the unloaded piezo in free air. When the transducer will be completed, the resonance frequency will be measured again with the transducer in the water.

The powerful (and free) BioSono KLM software has been used to model the transducer performance. From the physical description of the transducer components, this software will calculate a whole range of outputs, including the resonance and antiresonance frequencies and impedances.

The model is in very good agreement with the measured frequencies, and calculates a resonance impedance of 0.37 ohm. This is in line with the piezo manufacturer figure of less than 1 ohm.

The design goal is to transmit a peak power of 12 W to the transducer. This means that during the pulses, a high-frequency AC current of 5.7 amperes will flow through the transducer. Usually, an impedance matching circuit would be placed inside the transducer housing so that the amplifier will see an impedance of 50 ohms with a reduced current ouput. The BioSono KLM software can be used to calculate the required impedance matching circuit.

However, for this project, the decision has been made to use a high-current Class-A amplifier with an output impedance matching the piezo’s impedance of 0.37 ohm.

There are 2 main advantages for this unusual design:

a)  The ouput current to the piezo will be a pure sinewave instead of the typical square wave used in continuously transmitting ultrasonic applications;

b) The amplifier will use a standard marine power supply voltage of 12 V.  With a higher impedance, a higher voltage power supply would be needed.

Class-A amplifiers are well known for their high-fidelity but poor efficiency (as low as 15%). In this application, this efficiency penalty is not significant, because the length of the pulses will be very short. Even with an instantaneous transmitting power of 12 W, the average consumed power will much less than 1 watt.

Doppler profiler: design considerations

With a pulse-to-pulse coherent Doppler profiler, we can pick a specific remote region where we want the measurement to be made. Here we plan to measure the average speed of water in a sample volume of 1 cm long situated at 1 meter from the transducer.

With a speed of sound through water of 1500 m/s, the time to a first echo from the beginning of the sample volume is 1333.3 μs. The time to a first echo from the end of the sample is 1346.7 μs.

To make a measurement, the 3 MHz transducer will send 2 pulses.

After sending the first pulse, the transducer will switch to receive mode and will sample the echo from exactly 1333.3 to 1346.7 μs after the beginning of the pulse. The microprocessor will digitize this echo with its internal 84 MHz ADC and store it in memory. Soon after, the transducer sends a 2^nd pulse and the process is repeated.  The second echo is also digitized and stored. As the particles in the water have moved between the 2 samples, the echoes will be separated by a phase angle ϕ (the Doppler shift).  From the stored data, the microprocessor will then calculate the Doppler shift (90 deg in the following figure).

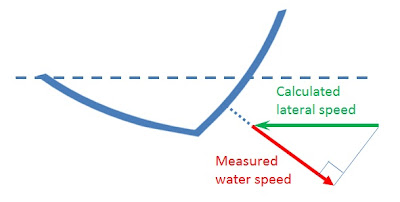
The Doppler shift is related to the component of the speed of the water in the axis of the ultrasonic beam. But there is a problem: more than one velocity value will produce the same Doppler shift.

To pick the right one, we need an external information. In our case, we will calculate an estimate of the lateral speed from the boat's K constant and the current values of boat speed and heel angle. We will then pick the profiler's measurement that is the closest to this estimate.

A custom coherent Doppler profiler

Here is a preliminary diagram of the prototype profiler that I plan to build.

I intend to modify an existing depth transducer, replacing the piezo disc by a 3 MHz one. This may be the trickiest part.

The frequency generator can be programmed to send either a constant frequency pulse or a variable frequency ('chirp') one. This may be useful later on.

The STM32F4 board will control the frequency generator, and will receive and analyze the echo signals. The STM32F4 microprocessor has built-in DSP (digital signal processing) capabilities.

The total hardware cost (with 2 transducers) should be less than 500 US$. Not too bad for near-America Cup performance, as this could develop in an open software project.

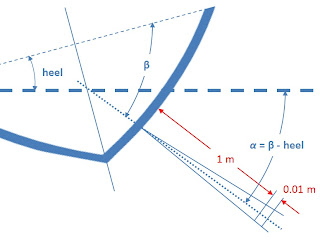
Measuring lateral speed (leeway)

It is possible to measure directly the lateral speed through water of a sailboat making leeway, by using a pulse-to-pulse coherent Doppler profiler. This is the technique used by the Volvo Ocean Race Puma team. In their case, the transducers are installed under the bulb keel.

For a conventional sailboat, a different arrangement can be used.

In the project that I am considering, 2 transducers will be able to measure the component of the speed of the water parallel to the axis of the ultrasonic beam at a distance of 30 cm from the hull.

By knowing the installation and the heel angles, it is then possible to calculate the lateral speed of the boat.

A good introduction to the pulse-to-pulse coherent Doppler technique can be found in these documents:

“Pure coherent Doppler systems – how far can we push it?”  Lohrman and Nylund, 2008.

“Performance of a Single-Beam Pulse-to-Pulse Coherent Doppler Profiler”  Zedel, Hay, Cabrera and Lohrmann, 1996.