One problem with MagCal is that one of the results (the matrix A) cannot be used directly. You have to calculate the inverse matrix A-1. The other problem is that the matrix A elements have a limited number of significant digits, which affects the precision of the inverted result. And finally, the raw measurements numbers cannot be greater than 99.99, so that you may have to scale down all your data to use it.
Magneto v1.2 can be downloaded here:
https://sites.google.com/view/sailboatinstruments1What are the differences between MagCal and Magneto?
Both find the equation of an ellipsoid that best fits the raw data points, using however different techniques. MagCal uses an “adaptive least square estimator”, and Magneto uses the “Li's ellipsoid specific fitting algorithm”. Which one is better? I don’t know, but the authors that have developed MagCal suggest in a recent paper that they may now use Li’s method.
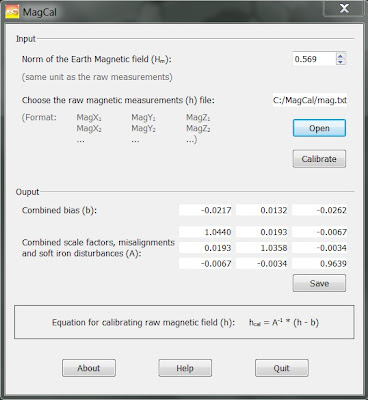
Here is the output of both softwares, using the same raw data file provided with MagCal.
As you can see, the results are nearly identical. I plan to add new features and to fully document Magneto on its hosting site when time permits.

Hi there, awesome site. I thought the topics you posted on were very interesting. I tried to add your RSS to my feed reader and it a few. take a look at it, hopefully I can add you and follow.
ReplyDeleteHello,
ReplyDeleteIs it possible to modify the source code ? Because I would like to implement the algorithm in an embedded system.
I can't save a lot of data in a file like in a pc, I have to execute the algorithm with only few data.
It is certainly possible, if you can find or develop an alternate math library (instead of Fortran) for matrix calculations. Matrix multiplication and inversion code are readily available, eigenvalues calculations may be harder to come by. I would strongly consider a 32-bit microprocessor for such a task.
ReplyDeleteFor those who have inquired on the possibility of porting the Magneto source code to an embedded system, here is a site with extensive matrix source code in C language:
ReplyDeletehttp://www.mymathlib.com/matrices/
Be aware that there is an important difference in the way the matrix elements are stored in memory between Fortran and C. In Fortran, the elements are stored column by column, while in C and C++, they are stored line by line.
And the Moore-Penrose pseudo-inverse may also be replaced by the normal matrix inverse, as they are normally the same for a square matrix, unless your data set is bad or incomplete.
I have taken a step further in porting the Magneto source code to 100% C-language. It is available at:
ReplyDeletehttps://sites.google.com/site/sailboatinstruments1/c-language-implementation
Very nice work. Helps me a lot to write a calibration routine for my lowcost MEMS-Magnetometer. Thank you for sharing.
ReplyDeleteHi Mr. Merlin
ReplyDeleteI am a bit confused about the input data. When you say 'raw data', does it mean the data come from ADC (whose unit is 'counts') ?
I've looked into your sample data (sample.txt), and i found the value of all data are less than 1 and greater than -1 .
How did you get this 'raw data' ?
do we have to calibrate the ADC output first using parameter provided in the datasheet?
Thank you for your support.
Magneto expects to receive raw data in +- format (a value of zero indicating a null field in the current axis), but not necessarily normalized to +-1.0.
DeleteIf your sensors have SPI or I2C outputs, they will usually directly produce the required format. For example, the MicroMag3 magnetometer directly produces counts from -3411 to +3411, and the the SCA3000 accelerometer directly produces counts from -1333 to 1333, and Magneto can process direcly these values, without the need to normalize them to +- 1.0. I understand that a normalization may be desirable to avoid machine precision problems, but this has not been the case with these sensors.
If your sensors produce voltage levels that you have to convert to counts with an ADC, you have indeed to substract a zero field value from the ADC output before using Magneto. You would then normally choose the maximum positive value as input to the 'Norm of Magnetic or Gravitational field'.
But this norm value is not critical if all you want to calculate later on is a heading (if it is a magnetometer) or a tilt angle (if it is an accelerometer). You can input any reasonable value for the norm, the correction matrix will be different by just a scaling factor, but the calculated heading (or tilt angle) will be the same, as it depends only on the relative value of the field components. The bias values will be unchanged, as they do not depend on the norm.
Could I ask you to explain how you find the value "norm of magnetic or gravitational field" please? This has a big effect on the results and I don't know how to find this value for the program. Thank you.
ReplyDeleteI am quoting a part of a previous answer as it is directly relevant to your question:
Delete"You would then normally choose the maximum positive value as input to the 'Norm of Magnetic or Gravitational field'.
But this norm value is not critical if all you want to calculate later on is a heading (if it is a magnetometer) or a tilt angle (if it is an accelerometer). You can input any reasonable value for the norm, the correction matrix will be different by just a scaling factor, but the calculated heading (or tilt angle) will be the same, as it depends only on the relative value of the field components. The bias values will be unchanged, as they do not depend on the norm."
In other words, inspect your output values and use the largest, which will likely represents the field magnitude when the sensor is aligned with it.
I am messing around with your C-based calibration tool magneto and am trying to feed it some simple data such as
ReplyDelete1 0 0
0 1 0
0 0 1
-1 0 0
0 -1 0
0 0 -1
.707106781 .707106781 0
0 .707106781 .707106781
.707106781 0 .707106781
I thought these are sampled on a perfect sphere. As expected I get a bias of 0 in all three axis. I would have expected to obtain an A^-1 as the identity. This is not so. What am I doing wrong?
Ignore me. You actually do get (almost) the identity. Since the data is on a sphere, the orientation for the elipsoid is not well defined. So it appears to be rotated by some (arbitrary?) orientation but still gives you the expected values h_cal for a choice if input h. A further mistake I made was to ignore the variable hm in the code which encodes for the above mentioned 'norm of magnetic or gravitational field'.
Deletei really want to do the same stuff but on the C# can you give me the algorithm of your code it have been 2 weeks i'm working on it and didn't found anything yet.
ReplyDeleteCan you help please
I got A-1 and b in the formula, how can I use it in a real application? Is there a related tutorial?
ReplyDeleteThis comment has been removed by the author.
ReplyDeleteThx for your sharing.
ReplyDeleteNice Post...........
ReplyDeleteBuy BILL COUNTER machine in Cambodia, Buy Euro USD GBP SAR LBP MYR KHR value counter machine, Buy ECB Teste Euro Fake Note Money Detector in Europe, Buy Two Pocket Banknote Sorting Machine for USD EUR GBP Multi Currency Money Sorter, Mix Value Counting Machine in Laos
I'm interested in your 100% C-language
ReplyDeleteI'm interested in your 100% C-language port of the Magneto code, but keep getting errors at the Google URL. Is there any other way to see the file(s)?
ReplyDeleteI am also interested and getting the error back from the link.
Deletei found the c code through some digging and here is a link to the .c file (it is just a command line tool, no gui) and a sample .txt file.
DeleteI modified the code slightly so that it takes command line arguments norm and name of text file.
https://limewire.com/d/ebb62605-02f6-425f-afdc-8d398f1cde2a#-Gg2Xm6PQz2S9xIScZbpfCosiSu9nbpgEIYu8fdxebE
The link is valid for 1 week but if you read this message, i can create a new one. Cheers
I am very interested, could you share another link? Thanks!
DeleteRespect and I have a tremendous proposal: Who To Contact For House Renovation house renovation price
ReplyDeleteDesign Essentials in Delhi, NCR- Front Elevation Design We are the Best Interior Designer In Commercial And residential areas in Delhi NCR.
ReplyDelete